3D Isometric Camera in Rust

In this blog post, I will go over my implementation of a 3D isometric camera in Rust using the Bevy game engine. I will also be dipping into some of the math involved when using an isometric projection.

Dependencies

To begin, you will need to add bevy as a dependency

# Cargo.toml

[dependencies]
bevy = "0.5"

Moving the player

In a regular 3D game, the player’s movement direction can be represented as a normalized vector $\vec v$ where $\| \vec v \| = 1$. So, for example, the vector $\vec v = (1, 0)$ may indicate that the player should go rightwards.

See the following snippet for an example of getting a movement direction (velocity):

fn player_movement(
    key_input: Res<Input<KeyCode>>,
    mut player_query: Query<
        (&mut RigidBodyVelocity, &RigidBodyMassProps, &Transform),
        With<Player>,
    >,
    time: Res<Time>,
) {
    if let Ok((mut rb_velocity, rb_mass_props, transform)) = player_query.single_mut() {
        let velocity = {
            let mut velocity = Vec3::ZERO;
            let local_z = transform.local_z();
            let forward = -Vec3::new(local_z.x, 0., local_z.z);
            let right = Vec3::new(local_z.z, 0., -local_z.x);

            for key in key_input.get_pressed() {
                match key {
                    KeyCode::W => velocity += forward,
                    KeyCode::S => velocity -= forward,
                    KeyCode::A => velocity -= right,
                    KeyCode::D => velocity += right,
                    _ => (),
                }
            }

            velocity.normalize()
        };
        // Move player in the direction of velocity.
    }
}

While this works for a standard perspective, some extra considerations must be taken into account when dealing with an isometric perspective.

In an isometric projection, the camera’s perspective is not parallel to the world’s axis. For example, let’s say we are trying to implement a simple player controller using WASD keys. What should happen when we press W? Take a look at this diagram depicting the player as a cube:

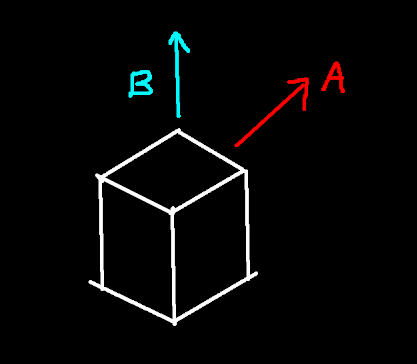
Game world from an isometric perspective

A naive implementation of this situation would result in the player moving along the $A$ direction, which is parallel to the world’s axis. However, the isometric perspective means that this movement direction is incorrect. The isometric projection places us at an angle to the world’s axis, meaning that the direction itself should be shifted as well. Intuitively, pressing W should move the player away from the camera (“upwards”) along the $B$ direction instead.

So how do we account for this? Well, let’s take a look at the same situation from a top-down perspective:

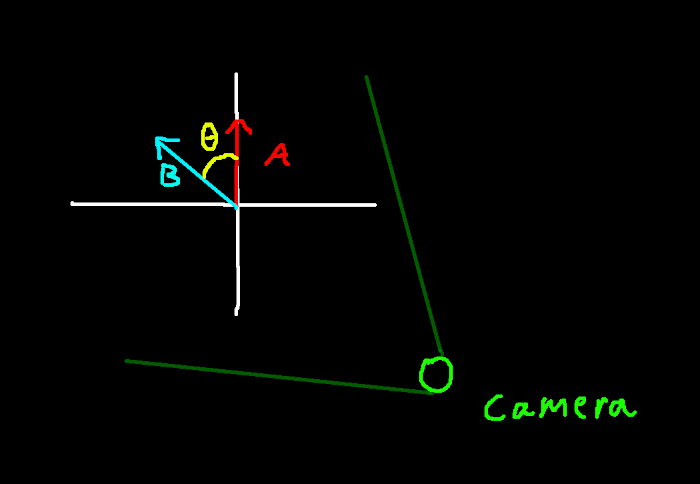
Top-down perspective of isometric perspective

As illustrated in the drawing above, the $A$ vector and $B$ vector are separated by an angle of $\theta$. So, to transform $A$ into $B$, $A$ must be shifted by $\theta$ anti-clockwise. The camera is rotated $45^\circ$ from the world’s axis, so we can set $\theta = 45^\circ = \frac{\pi}{4}$.

Given that $A = (0, 1)$ and $B$ is in the second quadrant, we can evaluate the value of $B$ like so:

$$\begin{align*} B &= (-\cos \theta, \, \sin \theta) \\ B &= (-\cos \frac{\pi}{4}, \, \sin \frac{\pi}{4}) \\ B &= (-\frac{\sqrt 2}{2}, \, \frac{\sqrt 2}{2}) \end{align*}$$

Now, let’s go through the rest for vectors of the form $\vec v = (x, y)$ where $x, y \in \mathbb{Z}$:

Original Vector	Transformation Vector
$(1, 0)$	$(\frac{\sqrt 2}{2}, \, \frac{\sqrt 2}{2})$
$(0, 1)$	$(\frac{-\sqrt 2}{2}, \, \frac{\sqrt 2}{2})$
$(-1, 0)$	$(\frac{-\sqrt 2}{2}, \, \frac{-\sqrt 2}{2})$
$(0, -1)$	$(\frac{\sqrt 2}{2}, \, \frac{-\sqrt 2}{2})$

Of course, we could just easily hard code this with a sequence of if statements, but that’s no fun! Anyways, it is important to generalize when considering the case where $x, y \in \mathbb{R}$

So how do we do this? Well, we could generalize by using a rotation matrix:

$$R = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}$$

Basically, applying this transformation matrix to our movement vector rotates the vector in a Cartesian plane by $\theta$ anti-clockwise. Just what we needed. Hence, by writing our movement vector as a column vector, we can apply the transformation by multiplying the two:

$$R \vec v = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \cos \theta - y \sin \theta \\ x \sin \theta + y \cos \theta \end{bmatrix}$$

Awesome, now we have a generalized formula to correct the movement direction! Or do we? Well, since this is a 3-dimensional world, it makes sense to apply the transformation to a Vec3 (vector with $3$ elements: $x$, $y$, and $z$). We are still talking about moving along the plane, so our $y$ coordinate (representing the height) should remain the same. So, our new transformation can be written like so:

$$R = \begin{bmatrix} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{bmatrix}$$ $$R \vec v = \begin{bmatrix} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x \cos \theta - z \sin \theta \\ y \\ x \sin \theta + z \cos \theta \end{bmatrix}$$

That’s better. Let’s start writing some code…

The first step is to assign the $3 \times 3$ rotation matrix to some variable. The rotation matrix can be derived using the function Mat3::from_axis_angle. This function takes a normalized rotation along with an angle to return a 3D rotation matrix, more explanation can be found here.

let rotation = Mat3::from_axis_angle(Vec3::new(0.0, 1.0, 0.0), 45_f32.to_radians());
dbg!(rotation);

This outputs the following to the console:

rotation = $mat3 {
    x_axis: Vec3(
        0.70710677,
        0.0,
        -0.70710677,
    ),
    y_axis: Vec3(
        0.0,
        1.0,
        0.0,
    ),
    z_axis: Vec3(
        0.70710677,
        0.0,
        0.70710677,
    ),
}

Thus, rotation is equal to the 3D rotation matrix we required.

Getting the correct direction is simply a matter of multiplication:

const PLAYER_SPEED: f32 = 128.0;
let isometric_velocity = rotation.mul_vec3(velocity * time.delta_seconds() * PLAYER_SPEED);

The original velocity is also multiplied by time.delta_seconds() to achieve continuous movement.

Camera implementation

A camera in an isometric game generally has two core responsibilities:

1. Follow the player.
2. Look at the player.

Follow the player

Following the player insinuates that the camera simply moves along with the player. We can accomplish this by setting the camera’s translation relative to the player’s translation. The camera must be offset by a fixed amount or else the camera would be inside the player:

const CAMERA_TRANSLATION_OFFSET: f32 = 20.0;
camera_transform.translation =
    player_transform.translation + Vec3::splat(CAMERA_TRANSLATION_OFFSET);

Running this within a system would successfully make the camera follow the player. We could optionally supplement this with some linear interpolation:

const CAMERA_TRANSLATION_OFFSET: f32 = 20.0;
camera_transform.translation = camera_transform.translation.lerp(
    player_transform.translation + Vec3::splat(CAMERA_TRANSLATION_OFFSET),
    0.01,
);

Look at the player

The simplest way to make the camera face the player is to use Transform::look_at:

camera_transform.look_at(player_transform.translation, Vec3::Y);

While this technically works, we can make this process frame rate independent by multiplying the change in movement by time.delta_seconds(). This makes the camera’s rotations smoother and avoids the game looking “jittery”.

const CAMERA_ROTATION_SPEED: f32 = 5.0;
let movement = (player_transform.translation - cam_state.current_target)
    * time.delta_seconds()
    * CAMERA_ROTATION_SPEED;
let new_target = cam_state.current_target + movement;
camera_transform.look_at(new_target, Vec3::Y);
cam_state.current_target = new_target;

This snippet relies on a resource (CamState) that keeps track of the camera’s previous target direction.