Isomorphism Classes of S-Decorated Simple Graphs

Edward Wibowo, Mar 20 2024

1. Introduction

This exploration will use the following definitions.

Using these definitions, we seek to explore the following question.

To aid our exploration, we define a way to categorize $l : V(G) \to S$ using ordered lists. We refer to these representations as the ordered list representation of $l$ .

For example, suppose $S = \{a, b\}$ and $G$ is a graph with $3$ vertices. If $l$ maps all vertices to $a$ , then the ordered list representation of $l$ is $[a, a, a]$ . If $l$ maps one vertex to $a$ and the other two to $b$ , then the ordered list representation of $l$ is $[a, b, b]$ . We note that the choice of which vertex is mapped to $a$ and which two are mapped to $b$ is irrelevant; any $l$ that maps one vertex to $a$ and the other two to $b$ is represented as $[a, b, b]$ .

Next, we observe that for any number of vertices $n$ and any $S$ , if $(G, l)$ is isomorphic to $(G^\prime, l^\prime)$ , then $l$ and $l^\prime$ share the same ordered list representation. This is formalized in the following lemma.

Proof. Suppose $(G, l)$ and $(G^\prime, l^\prime)$ are $S$ -decorated isomorphic. Then, there exists an isomorphism $\phi$ from $G$ to $G^\prime$ such that $l(v) = l^\prime(\phi(v))$ for all $v \in V(G)$ . Without loss of generality, suppose we enumerate $G$ and $G^\prime$ as $V(G) = \{v_1, v_2, \ldots, v_n\}$ and $V(G^\prime) = \{u_1, u_2, \ldots, u_n\}$ such that $\phi(v_i) = u_i$ for all valid $i$ . Then, we write the following equalities:

l(v_1) = l^\prime(\phi(v_1)) = l^\prime(u_1) \\ l(v_2) = l^\prime(\phi(v_2)) = l^\prime(u_2) \\ \vdots \\ l(v_n) = l^\prime(\phi(v_n)) = l^\prime(u_n).

Using the above equalities, the lists

[l(v_1), l(v_2), \ldots, l(v_n)] \quad\text{and}\quad [l^\prime(u_1), l^\prime(u_2), \ldots, l^\prime(u_n)]

must have the same elements in the same order. So, these lists must be identical. Hence, $l$ and $l^\prime$ must share the same ordered list representation.

□

2. Example Case

To achieve a better understanding of the problem, we count the number of isomorphism classes of $S$ -decorated simple graphs with $3$ vertices and $|S| = 2$ . By Definition 2, an isomophism between two $S$ -decorated simple graphs $(G, l)$ and $(G^\prime, l^\prime)$ implies $G$ is isomorphic to $G^\prime$ . Contrapositively, if $G$ is not isomorphic to $G^\prime$ , then $(G, l)$ and $(G^\prime, l^\prime)$ are not $S$ -decorated isomorphic regardless of the choice of $l$ and $l^\prime$ . Hence, we will count the number of $S$ -decorated isomorphism classes for each of the $4$ isomorphism classes of simple graphs with $3$ vertices.

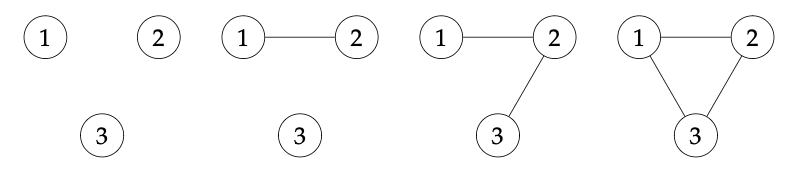
Figure 1. The four isomorphism classes of simple graphs with $3$ vertices.

Without loss of generality, let $S = \{a, b\}$ .

We start with the first isomorphism class, which consists of simple graphs with $3$ vertices and no edges. We can enumerate all possible ordered list representations of $l$ as follows:

$[a, a, a]$
$[a, a, b]$
$[a, b, b]$
$[b, b, b]$

We note that any graph with $3$ vertices and no edges are isomorphic, and the isomorphism can be any bijection between the two vertex sets. This means $(G, l)$ and $(G^\prime, l^\prime)$ should be $S$ -decorated isomorphic if $l$ and $l^\prime$ share the same ordered list representation as we can just pair up same-labelled vertices in $G$ and $G^\prime$ .

We capture this line of reasoning in the following lemma

Proof. Suppose $l$ and $l^\prime$ share the same ordered list representation. We shall construct an isomorphism $\phi : V(G) \to V(G^\prime)$ such that $l(v) = l^\prime(\phi(v))$ for all $v \in V(G)$ .

Since $l$ and $l^\prime$ share the same ordered list representation, we can create $n$ distinct pair of vertices $(v, u)$ where $v \in V(G)$ and $u \in V(G^\prime)$ such that their labels match (so $l(v) = l^\prime(u)$ ). We can do this in a way such that no two pairs share the same vertex in $G$ or $G^\prime$ since $l$ and $l^\prime$ have the same ordered list representation and $|V(G)| = |V(G^\prime)|$ . Then, we can define $\phi$ to be the function that maps $v$ to $u$ for each pair $(v, u)$ .

We justify that $\phi$ is a bijection. Since no two pairs share the same vertex in $G$ or $G^\prime$ , $\phi$ pairs each element of $V(G)$ with exactly one element of $V(G^\prime)$ and vice versa. Hence, $\phi$ is a bijection.

Since $G$ and $G^\prime$ are defined to be simple graphs such that any bijection from $V(G)$ to $V(G^\prime)$ is a graph isomorphism, $\phi$ is also an isomorphism from $G$ to $G^\prime$ . Lastly, by construction, we have $l(v) = l^\prime(\phi(v))$ for all $v \in V(G)$ .

Therefore, $(G, l)$ and $(G^\prime, l^\prime)$ are $S$ -decorated isomorphic.

□

Using both Lemma 6 and Lemma 5, each of the four ordered list representations of $l$ corresponds to a unique isomorphism class of $S$ -decorated simple graphs. Thus, there are $4$ isomorphism classes of $S$ -decorated simple graphs with $3$ vertices and no edges.

We also note that for any graphs $G$ and $G^\prime$ in the isomorphism class consisting of graphs with $3$ vertices and $3$ edges (so the fourth one depicted in Figure 1), any bijection from $V(G)$ to $V(G^\prime)$ is a graph isomorphism. So, by Lemma 6 and Lemma 5, the number of isomorphism classes of $S$ -decorated simple graphs with $3$ vertices and $3$ edges is also $4$ .

Now, we need to count the $S$ -decorated isomorphism classes of simple graphs with $3$ vertices and $1$ or $2$ edges.

We analyze the second isomorphism class, which consists of simple graphs with $3$ vertices and $1$ edge. Lemmas 6 and 5 do not apply here since, for example, if the singular edge of $G$ maps to $a$ and the singular edge of $G^\prime$ maps to $b$ , then there is no $S$ -decorated isomorphism between $(G, l)$ and $(G^\prime, l^\prime)$ . We count by cases of the ordered list representation of $l$ by considering the possible labelling of the unique singular disconnected vertex.

Case $[a, a, a]$ : If both $l$ and $l^\prime$ map all vertices to $a$ , then any graph isomorphism between $G$ and $G^\prime$ will also preserve the $S$ -decoration. Thus, this case has $1$ isomorphism class.
Case $[a, a, b]$ : There would be $2$ isomorphism classes in this case. The first class is where the singular disconnected vertex maps to $b$ and the other two vertices map to $a$ . The second class is where the singular disconnected vertex maps to $a$ and the other two vertices map to $a$ and $b$ .
Case $[a, b, b]$ : Similar to the previous case, there would be $2$ isomorphism classes in this case. The first case is where the singular disconnected vertex maps to $a$ and the other two vertices map to $b$ . The second case is where the singular disconnected vertex maps to $b$ and the other two vertices map to $a$ and $b$ .
Case $[b, b, b]$ : This is equivalent to the first case, so there is $1$ isomorphism class.

So, in total, there are $6$ isomorphism classes of $S$ -decorated simple graphs with $3$ vertices and $1$ edge.

The same logic can be applied to the third isomorphism class, which consists of simple graphs with $3$ vertices and $2$ edges. In this case, the unique vertex would be the one with degree $2$ . Hence, there are $6$ isomorphism classes of $S$ -decorated simple graphs with $3$ vertices and $2$ edges.

Therefore, our results can be summarized as follows:

Number of edges	Number of $S$ -decorated isomorphism classes
$0$	$4$
$1$	$6$
$2$	$6$
$3$	$4$

Table 1. The number of isomorphism classes of $S$ -decorated simple graphs with $3$ vertices.

bringing the total number of isomorphism classes of $S$ -decorated simple graphs with $3$ vertices to $20$ .

3. Linear Graphs

We further the exploration by answering Question 3 for linear graphs (i.e. paths) with $n$ vertices. More formally,

By definition, a linear graph is a simple graph with $n$ vertices and $n-1$ edges whose vertices can be ordered in a linear sequence such that the edges are between consecutive vertices in the sequence.

Figure 2. A linear graph with $5$ vertices.

We define the notion of a label sequence of an $S$ -decorated linear graph.

We note that depending on the choice of which of the two endpoints is $v_1$ and which is $v_n$ , the label sequence of a linear graph can be either $L_l(G)$ or $L_l(G)^R$ . Using this definition, we provide and prove the following theorem about the label sequences of $S$ -decorated linear graphs.

Proof. Without loss of generality, suppose $G$ is a path $v_1, v_2, \ldots, v_n$ and $G^\prime$ is a path $u_1, u_2, \ldots, u_n$ . We note

L_l(G) = [l(v_1), l(v_2), \ldots, l(v_n)] \quad\text{and}\quad L_{l^\prime}(G^\prime) = [l^\prime(u_1), l^\prime(u_2), \ldots, l^\prime(u_n)].

We prove both directions of the biconditional statement.

$\implies$ Suppose $(G, l)$ and $(G^\prime, l^\prime)$ are $S$ -decorated isomorphic. Then, there exists an isomorphism $\phi$ from $G$ to $G^\prime$ such that $l(v) = l^\prime(\phi(v))$ for all $v \in V(G)$ .

Let $\phi$ be an arbitrary $S$ -deocrated isomorphism from $(G, l)$ to $(G^\prime, l^\prime)$ . Since $\phi$ is edge-preserving, it must map $v_1$ (an endpoint of $G$ ) to either endpoint of $G^\prime$ (so either $u_1$ or $u_n$ ). We consider the two cases separately.

Case: $\phi$ maps $v_1$ to $u_1$ : Since $\phi$ is an $S$ -decorated isomorphism, $l(v_1) = l^\prime(\phi(v_1)) = l^\prime(u_1)$ . Furthermore, since $\phi$ is edge-preserving, it forces $\phi(v_2) = u_2$ , so we also know $l(v_2) = l^\prime(u_2)$ . We continue this reasoning for all pairs of vertices in $G$ and $G^\prime$ , allowing us to conclude $L_l(G) = L_{l^\prime}(G^\prime)$ .
Case: $\phi$ maps $v_1$ to $u_n$ : Similarly, since $\phi$ is an $S$ -decorated isomorphism, $l(v_1) = l^\prime(\phi(v_1)) = l^\prime(u_n)$ . This forces $\phi(v_2) = u_{n-1}$ , so we also know $l(v_2) = l^\prime(u_{n-1})$ . Continuing this reason, we find that the lists
$L_l(G) = [l(v_1), l(v_2), \ldots, l(v_n)] \quad\text{and}\quad \\ L_{l^\prime}(G^\prime) = [l^\prime(u_n), l^\prime(u_{n-1}), \ldots, l^\prime(u_1)]$
are identical. Consequently, we have $L_l(G) = L_{l^\prime}(G^\prime)^R$ .

Thus, in both cases, we have $L_l(G) = L_{l^\prime}(G^\prime)$ or $L_l(G) = L_{l^\prime}(G^\prime)^R$ .

$\impliedby$ Suppose $L_l(G) = L_{l^\prime}(G^\prime)$ or $L_l(G) = L_{l^\prime}(G^\prime)^R$ . We argue by cases:

Case: $L_l(G) = L_{l^\prime}(G^\prime)$ : In this case, we shall construct an $S$ -decorated isomorphism $\phi$ from $G$ to $G^\prime$ . Let $\phi : V(G) \to V(G^\prime)$ be the function that maps $v_i \in V(G)$ to $u_i \in V(G^\prime)$ for all valid $i$ .

$\phi$ is bijective by construction since it pairs each element of either $V(G)$ or $V(G^\prime)$ with exactly one element of the other set. Furthermore, since $G$ is defined as a path $v_1, v_2, \ldots, v_n$ and $G^\prime$ is defined as a path $u_1, u_2, \ldots, u_n$ , $\phi$ is also edge-preserving.

Since $L_l(G) = L_{l^\prime}(G^\prime)$ , we have $l(v_i) = l^\prime(u_i)$ for all valid $i$ . Since each $u_i = \phi(v_i)$ , we also have $l(v_i) = l^\prime(\phi(v_i))$ for all valid $i$ . Thus, $\phi$ is an $S$ -decorated isomorphism from $(G, l)$ to $(G^\prime, l^\prime)$ .
Case: $L_l(G) = L_{l^\prime}(G^\prime)^R$ : Likewise, we construct an $S$ -decorated isomorphism $\phi$ from $G$ to $G^\prime$ . Let $\phi : V(G) \to V(G^\prime)$ be the function that maps $v_i$ to $u_{n-i+1}$ for all valid $i$ .

$\phi$ is bijective by construction since it pairs each element of either $V(G)$ or $V(G^\prime)$ with exactly one element of the other set. Moreover, we can view $\phi$ as relabelling the vertices of $G$ from $v_1, v_2, \ldots, v_n$ to $u_n, u_{n-1}, \ldots, u_1$ . The resulting graph forms the path $u_1, u_2, \ldots, u_n$ which is exactly $G^\prime$ , so $\phi$ is also edge-preserving.

Since $L_l(G) = L_{l^\prime}(G^\prime)^R$ , we have $l(v_i) = l^\prime(u_{n-i+1})$ for all valid $i$ . Since each $u_{n-i+1} = \phi(v_i)$ , we also have $l(v_i) = l^\prime(\phi(v_i))$ for all valid $i$ . Thus, $\phi$ is an $S$ -decorated isomorphism from $(G, l)$ to $(G^\prime, l^\prime)$ .

In both cases, we have constructed an $S$ -decorated isomorphism from $(G, l)$ to $(G^\prime, l^\prime)$ . Therefore, $(G, l)$ and $(G^\prime, l^\prime)$ are $S$ -decorated isomorphic.

Since both directions of the biconditional statement have been proven, the lemma is proven.

□

With Theorem 9, we have reduced the problem of counting the number of isomorphism classes of $S$ -decorated linear graphs to counting the number of label sequences, treating sequences that are reverses of each other as identical.

Each label sequence is a sequence of $n$ elements, where each element could possibly be any of the $|S|$ elements. So, there are $|S|^n$ possible label sequences.

Sequences that form a palindrome do not have a reverse that is distinct from itself. So each palindromic sequence contributes to a new isomorphism class of $S$ -decorated linear graphs. Sequences that do not form a palindrome have a reverse that is distinct from itself, so we must divide the number of sequences that do not form a palindrome by $2$ to avoid overcounting. Thus, the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices is

\text{\# of palindromic sequences} + \frac{\text{\# of non-palindromic sequences}}{2}.

We note that the number of non-palindromic sequences can be calculated as

|S|^n - \text{\# of palindromic sequences}.

Thus, we seek to count the number of palindromic sequences.

A palindrome is completely determined by the first half of the sequence. So for an even length sequence, the number of palindromic sequences is the same as the number of sequences of half the length. For an odd length, the number of palindromic sequences is the same as the number of sequences of half the length, except that the middle element can be any of the $|S|$ elements. To capture this line of reasoning, we have:

\text{\# of palindromic sequences} = |S|^{\text{ceil}(n/2)}.

Therefore, the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices is

=|S|^{\text{ceil}(n/2)} + \frac{|S|^n - |S|^{\text{ceil}(n/2)}}{2} \\ = \frac{|S|^n + |S|^{\text{ceil}(n/2)}}{2}.

Using this formula, we can tabulate the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices for various $n$ and $|S|$ . Arbitrarily, we choose $n = 4$ . The results are tabulated as follows:

\| $S$ \|	Number of $S$ -decorated isomorphism classes
$1$	$1$
$2$	$10$
$3$	$45$
$4$	$136$
$5$	$325$
$6$	$666$
$7$	$1225$
$8$	$2080$
$9$	$3321$
$10$	$5050$

Table 2. The number of isomorphism classes of $S$ -decorated linear graphs with $4$ vertices.

From Table 2, we can conclude that as $|S|$ increases, the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices increases. Introducing more elements to $S$ increases the number of ways to label the vertices of the linear graph, which in turn increases the number of isomorphism classes of $S$ -decorated linear graphs.

3.1. Counting Isomorphism Classes through Ordered List Representations

Although we have already found that the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices is

\frac{|S|^n + |S|^{\text{ceil}(n/2)}}{2}

it would still be interesting to explore how the number of isomorphism classes can be counted through the ordered list representations of the labelling functions (as defined in Definition 4.

First, we note that finding the number of ordered list representations is equivalent to finding the number of ways to choose $n$ elements from a set of $|S|$ elements with repetition. Therefore, the number of ordered list representations for $l : V(G) \to S$ where $|V(G)| = n$ is

\binom{|S| + n - 1}{n}.

Next, for each of these $\binom{|S| + n - 1}{n}$ ordered list representations, we can apply Theorem 9 to determine whether the corresponding $S$ -decorated linear graph is in a new isomorphism class. This is equivalent to checking the number of palindromes and non-palindromes that can be made from each ordered list representation.

Thus, given an arbitrary labelling function $l$ , we seek to count the number of palindromes (which also would help us count the number of non-palindromes) that can be made from its ordered list representation. We consider two cases of the parity of the length of $l$ ‘s ordered list representation which is equal to $|V(G)| = n$ :

Case: $n$ is even: For there to be a palindrome of even length, the first half of the sequence must be the reverse of the second half. This means the frequency of an element in the first half must be the same as the frequency of the same element in the second half. Thus, each distinct element in $l$ ‘s ordered list representation must have an even frequency for there to be at least one palindrome. Else, there would be no palindromes.

Further, since each palindrome is completely determined by the first half, the number of palindromes would be equal to the multinomial coefficient of half of the length and half of each frequency of the elements in $l$ ‘s ordered list representation. Symbolically,
$= \binom{n/2}{\frac{f_1}{2}, \frac{f_2}{2}, \ldots, \frac{f_{|S|}}{2}}$
where each $f_i$ is the frequency of the $i$ th element of $S$ in $l$ ‘s ordered list representation.
Case: $n$ is odd: The only way to form a palindrome from $l$ ‘s ordered list representation is if exactly one element has an odd frequency and the rest have even frequencies. The one element with odd frequency can be placed in the middle of the sequence. If there is either no element with an odd frequency or more than one element with an odd frequency, then there would be no palindromes.

If there is exactly one element with odd frequency in $l$ ‘s ordered list representation, then the number of palindromes can be calculated by the even-length case, where the length is $n - 1$ and the frequency of the odd element is $f_i - 1$ .

To summarize, the algorithm to count the number of palindromes by ordered list representation is as follows:

Iterate through each of the $\binom{|S| + n - 1}{n}$ possible ordered list representations of $l$ .
For each ordered list representation calculate the number of palindromes:
- Count the frequency of each element in the ordered list representation.
- If $n$ is even: if there exists an element of odd frequency, the number of palindromes is $0$ . Else, the number of palindromes is $\binom{n/2}{\frac{f_1}{2}, \frac{f_2}{2}, \ldots, \frac{f_{|S|}}{2}}$ where each $f_i$ is the frequency of the $i$ th element of $S$ in the ordered list representation.
- If $n$ is odd: if there is more than one element with odd frequency, or there is no element with odd frequency, the number of palindromes is $0$ . Else, consider the even-length case where the length is $n - 1$ and the frequency of the odd element is $f_i - 1$ .
For each ordered list representation: increment the running total by the number of palindromes added with the number of non-palindromes divided by $2$ .
- The total number of arrangements is $\binom{n}{\frac{f_1}{2}, \frac{f_2}{2}, \ldots, \frac{f_{|S|}}{2}}$ where each $f_i$ is the frequency of the $i$ th element of $S$ in the ordered list representation. So, the number of non-palindromes would be equal to $\binom{n}{\frac{f_1}{2}, \frac{f_2}{2}, \ldots, \frac{f_{|S|}}{2}}$ subtracted by the number of palindromes.
Return the running total.

This algorithm can be used to count the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices. The implementation of this algorithm can be found in the appendix.

4. Literature: Weisfeiler-Lehman Algorithm

When given two $S$ -decorated graphs $(G, l)$ and $(G^\prime, l^\prime)$ , one might want to determine whether they are $S$ -decorated isomorphic in an efficient manner. We can observe that when $|S| = 1$ , this problem reduces to the graph isomorphism problem.

When $|S| = 1$ , all vertices are mapped to the same singleton element. So, any isomorphism between $G$ and $G^\prime$ will also preserve the $S$ -decoration. Thus, $(G, l)$ and $(G^\prime, l^\prime)$ are $S$ -decorated isomorphic if and only if $G$ and $G^\prime$ are isomorphic.

However, as stated in [2], there is no known efficient (polynomial time) algorithm for the graph isomorphism problem. If we could find an efficient polynomial time algorithm for the $S$ -decorated isomorphism problem, we would have also solved the graph isomorphism problem in polynomial time.

Although determining definitively whether two graphs are isomorphic is difficult, there are heuristic procedures that can be used to determine whether two graphs are not isomorphic or inconclusively isomorphic. One such example is the Weisfeiler-Lehman algorithm.

As described in [1], there are many variations of the algorithm, but in the simplest $1$ -dimensional form, the algorithm works as follows:

Assign each vertex a color, initially based on its degree.
At each subsequent iteration, update each vertex’s color based on its color in the previous iteration and the multiset of colors of its neighbors.
Continue iterating until the colors stabilize, meaning that no vertex’s color changes from one iteration to the next.

Given two graphs, if the colors stabilize to different colorings, then the graphs are not isomorphic. However, if the colors stabilize to the same coloring, then the graphs may or may not be isomorphic; the answer is inconclusive. In this way, the algorithm does not completely solve the graph isomorphism problem, but it can be used as a heuristic to determine non-isomorphism.

Furthermore, this algorithm is generalizable as detailed in [1, 1.2] to higher dimensions, where higher dimensional Weisfeiler-Lehman algorithms can determine non-isomorphism for a larger class of graphs.

However, [1, 2.1] cites counterexamples to the Weisfeiler-Lehman algorithm, where the algorithm fails to determine non-isomorphism for certain classes of graphs. Hence, regardless of the dimension of the Weisfeiler-Lehman algorithm, there will always be non-isomorphic graphs for which the algorithm cannot determine non-isomorphism. This represents a fundamental limitation of the traditional Weisfeiler-Lehman algorithm.

To address this limitation, [1] introduces a recursive $k$ -dim Weisfeiler-Lehman algorithm. This modification refines the Weisfeiler-Lehman algorithm and is able to determine non-isomorphism for the aforementioned counterexamples.

4.1 Application to $S$ -Decorated Isomorphisms

The idea of finding efficient ways to determine non-isomorphism is intriguing and can be applied to the $S$ -decorated isomorphism problem. For example, suppose we seek to determine whether two $S$ -decorated graphs $(G, l)$ and $(G^\prime, l^\prime)$ are not $S$ -decorated isomorphic or inconclusively $S$ -decorated isomorphic. A potential approach is to first check whether $l$ and $l^\prime$ share the same ordered list representation as mentioned in Lemma 5. If they do not, we can safely conclude that $(G, l)$ and $(G^\prime, l^\prime)$ are not $S$ -decorated isomorphic. If $l$ and $l^\prime$ do share the same ordered list representation, then we can apply the recursive $k$ -dim Weisfeiler-Lehman algorithm to determine non-isomorphism.

Checking if two ordered lists are equal can be done efficiently. So, having this check as a preliminary step could save computation time in certain cases by avoiding the recursive $k$ -dim Weisfeiler-Lehman algorithm.

5. Appendix

The following is the implementation of the algorithm to count the number of isomorphism classes of $S$ -decorated linear graphs with $n$ vertices through the possible ordered list representations of the labelling functions. Comments have been added for additional explanation.

import itertools
import math
from typing import List


def multinomial_coefficient(n: int, k: List[int]) -> int:
    """
    Compute the multinomial coefficient of n and k.
    """
    assert sum(k) == n
    return math.factorial(n) // math.prod(math.factorial(i) for i in k)


assert multinomial_coefficient(4, [2, 2]) == 6
assert multinomial_coefficient(4, [1, 1, 2]) == 12
assert multinomial_coefficient(4, [4]) == 1
assert multinomial_coefficient(7, [2, 1, 4]) == 105


def count_palindromes(k: List[int]) -> int:
    """
    Count the number of palindromes in a list of integers.
    """
    n = len(k)
    freqs = {x: k.count(x) for x in k}

    if n % 2 == 0:
        # n is even
        if any(x % 2 != 0 for x in freqs.values()):
            # If any number appears an odd number of times, it would be impossible to form a palindrome.
            # Since n is even, a given number should appear the same number of times on both halves of the palindrome.
            # So, for there to be a palindrome, all numbers should appear an even number of times.
            return 0
        # A palindrome is completely determined by the structure of the first half.
        # So, the number of palindromes would be the multinomial coefficient of n // 2 and half the frequency of each number.
        return multinomial_coefficient(n // 2,
                                       [x // 2 for x in freqs.values()])

    # n is odd
    odd_freqs = [x for x in freqs if freqs[x] % 2 != 0]
    # If n is odd, the only way to form a palindrome is if exactly one number appears an odd number of times.
    # We can put this number in the middle of the palindrome.
    # Then, the number of palindromes would be the number of ways to form a palindrome with the remaining numbers
    # (of which there are an even number of each).
    if len(odd_freqs) != 1:
        return 0
    k.remove(odd_freqs[0])
    return count_palindromes(k)


assert count_palindromes([1, 1, 1, 1]) == 1
assert count_palindromes([0, 0, 1, 1]) == 2
assert count_palindromes([0, 0, 0, 1]) == 0
assert count_palindromes([1, 1, 2, 2, 3, 3]) == 6
assert count_palindromes([1, 1, 1, 2, 2, 3, 3]) == 6
assert count_palindromes([1, 1, 1, 2, 2, 2, 3]) == 0


def count_linear_s_decorated_iso_classes(n: int, k: int) -> int:
    """
    Count the number of linear S-decorated isomorphism classes of linear graphs with n vertices and |S| = k.
    """
    ordered_list_representations = itertools.combinations_with_replacement(
        range(k), n)
    iso_classes = 0
    for rep in ordered_list_representations:
        # For each ordered list representation, count the number of arrangements, treating lists that are reverses of each other as the same.
        total = multinomial_coefficient(n, [rep.count(x) for x in range(k)])
        palindromes = count_palindromes(list(rep))
        # Each arrangement is either a palindrome or non-palindrome.
        # So, we can compute the number of non-palindromes by subtracting the number of palindromes from the total.
        non_palindromes = total - palindromes

        # Each non-palindrome arrangement can be grouped with its reverse to form an isomorphism class.
        # So, the number of isomorphism classes is the sum of the number of palindromes and half the number of non-palindromes.
        iso_classes += palindromes + non_palindromes // 2
    return iso_classes


assert count_linear_s_decorated_iso_classes(4, 1) == 1
assert count_linear_s_decorated_iso_classes(11, 1) == 1
assert count_linear_s_decorated_iso_classes(4, 2) == 10
assert count_linear_s_decorated_iso_classes(3, 3) == 18

The following is a program that compares three implementations to count the number of $S$ -decorated isomorphism classes of linear graphs with $n$ vertices.

Formulaic method using $\frac{|S|^n + |S|^{\text{ceil}(n/2)}}{2}$ .
Algorithmic method through considering possible ordered list representations using the above algorithm.
Brute force method that lists through all possible lists and removes ones that are reverses of each other.

Running the code reveals that all three methods produce the same results. However, the formulaic method is the most efficient, followed by the algorithmic method, and then the brute force method.

import itertools


def remove_reversals(possible_lists):
    iso = []
    for l in possible_lists:
        is_iso = True
        for r in iso:
            if l == r[::-1] or l == r:
                is_iso = False
                break
        if is_iso:
            iso.append(l)
    return iso


def count_iso(n, k):
    possible_lists = list(itertools.product(range(k), repeat=n))
    # Remove lists that are reversals of each other
    iso = remove_reversals(possible_lists)
    return len(iso)


import algorithm
import math

n = 4

for s in range(1, 11):
    formula_ans = (s**n + s**math.ceil(n / 2)) / 2
    algorithm_ans = algorithm.count_linear_s_decorated_iso_classes(n, s)
    brute_ans = count_iso(n, s)
    print("n = ", n, "k = ", s)
    print("Formula: ", int(formula_ans))
    print("Algorithm: ", algorithm_ans)
    print("Brute: ", brute_ans)

References

[1] B. L. Douglas. The weisfeiler-lehman method and graph isomorphism testing. 2011.

[2] S. Fortin. The Graph Isomorphism Problem. 1996.