Planes: altitude, roll, and collisions

Edward Wibowo, Feb 04 2022

Recently, I developed a game aptly titled “planes”. You can find the source code here.

Simply put, players of planes control a plane, swerving left and right, to dodge incoming obstacles. Although it may not be the most inventive game concept, I think the process of developing the game taught me a few important things. The game marked my first move in making an actual 3D game in bevy, rather than just toying around with physics and physically based rendering. Through developing planes, I went through the motions of thinking about a game concept, trying to implement it, and adding a final layer of polish.

The game is straightforward by nature; something I have learned after developing a few games here and there is to start small. Personally, an unhealthy amount of ambition to create my “dream game” first try makes me stagnant and inefficient. By starting with a small idea, I avoid trying to perfect everything I do.

Varying Altitude and Roll

One of the first things I did was make the plane rotate and sway as it moved left and right.

At the beginning of the development process, the initial rush of seeing a model I created in my game quickly diminished when I realized it was just a stagnant model moving left and right. Although moving left and right is all the player does in the game, I felt that I needed to add a bit of action to make the game more visually interesting.

Firstly, I wanted to slightly vary the height at which the plane flies as it moves left and right. Once the plane reaches either extremity, I wanted the plane to move to a slightly higher altitude. In essence, I wanted the plane’s altitude to vary like a parabola:

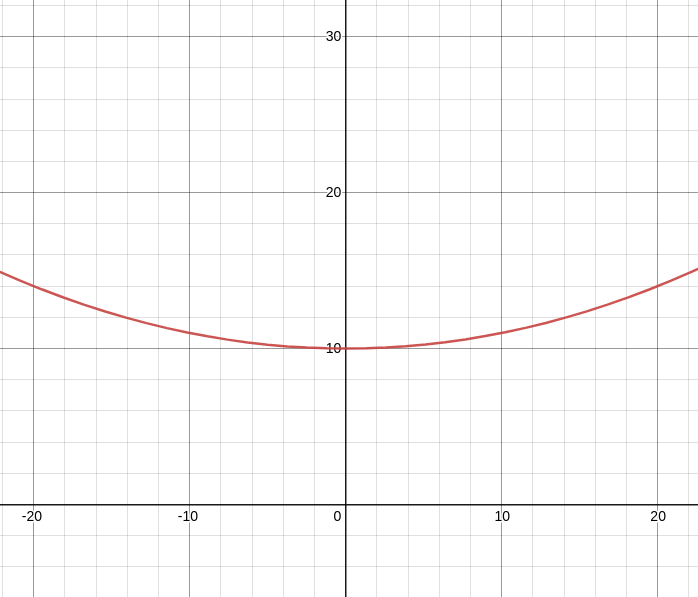
Graphed above is the function $f(x)$ , which represents the plane’s altitude at a given $x$ -coordinate. I defined it as $f(x) = 10 + 0.01x^2$ . At the center of the screen, the plane’s altitude is equal to $f(0) = 10$ . On either of the extreme sides (which is clamped in the range $|x| \leq 20$ ), the plane’s altitude is equal to $f(20) = f(-20) = 14$ . In code, this is written like so:

fn control_plane(
    mut transform: Query<&mut Transform, With<Plane>>,
) {
    let mut transform = transform.single_mut();

    // Update y translation relative to x translation
    transform.translation.y = ALTITUDE + 0.01 * transform.translation.x.powi(2);
}

However, even with this slight variation in altitude, the game still felt a little boring. So, in addition to varying the plane’s altitude, I also varied the plane’s rotation. To be more specific, I varied the plane’s roll. Similar to how I evaluated a function to derive the plane’s altitude, I used another function to calculate the roll angle:

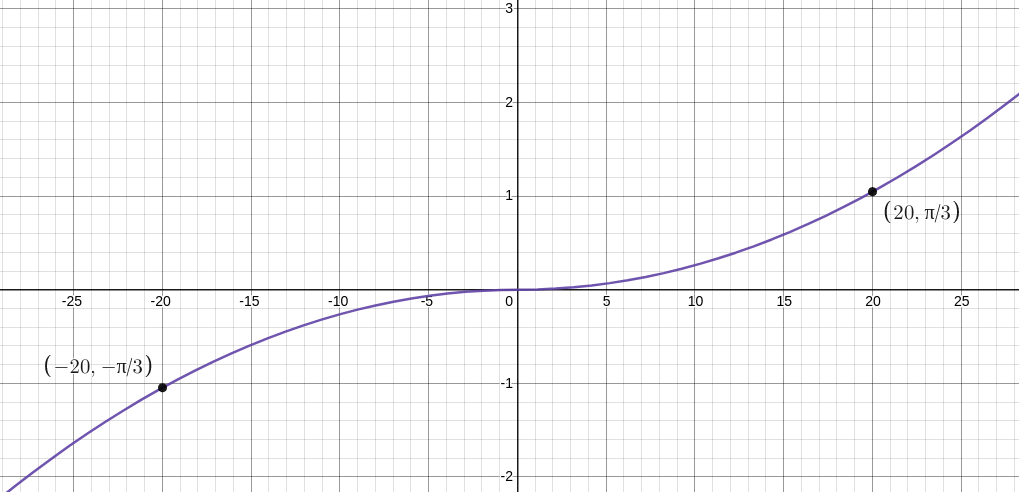
As graphed above, I used the function $g(x) = \frac{x |x|}{20^2} \cdot \frac{\pi}{3}$ to evaluate the plane’s rotation (along the $z$ axis in the game world). I used $x |x|$ in the function as opposed to $x^2$ to preserve the sign of $x$ . This meant that the value $g(x)$ outputs is different depending on if the plane is located left or right of the screen.

Left side of the screen: $g(-20) = \frac{-20 |-20|}{20^2} \cdot \frac{\pi}{3} = -\frac{\pi}{3}$
Center of the screen: $g(0) = 0$ (equivalent to no roll rotation)
Right side of the screen: $g(20) = \frac{20 |20|}{20^2} \cdot \frac{\pi}{3} = \frac{\pi}{3}$

Code-wise, this is what the roll function looks like:

fn rotate_plane(time: Res<Time>, mut transform: Query<&mut Transform, With<Plane>>) {
    let mut transform = transform.single_mut();

    let roll_offset = (PI / 24.0) * (time.time_since_startup().as_secs_f32() * ROLL_SPEED).sin();

    transform.rotation = Quat::from_rotation_z(
        (transform.translation.x * transform.translation.x.abs() * PI)
            / (3.0 * MAXIMUM_OFFSET.powi(2))
            + roll_offset,
    );
}

I also added a roll_offset, which continuously varies the roll of the plane to make it look like it is being affected by natural wind patterns.

All in all, the slight variations in altitude and roll made the game feel a little more alive (but has no effect on actual game mechanics).

Detecting Collisions

Implementing collision detection took me a while.

When I first approached collision detection, I decided to use a physics plugin called bevy_rapier. This plugin provides a whole suite of physics functions ranging from rigid bodies, joints, friction, and (of course) collision detection. However, after trying to integrate the plugin into my game, I found that I didn’t need many of the advanced features the library offered - I only needed to know when the plane collided with an obstacle. Further, introducing bevy_rapier as a dependency caused undesirable increases in compile time.

So, I set my eyes on heron: an “ergonomic physics API for bevy games”. heron’s interface was much simpler to use; however, at the time of writing this blog post, it is incapable of rendering 3D collision shapes. If it wasn’t for this limitation, I probably would have opted to use this library in the end…

Instead, I decided to write a custom collision detection plugin.

Custom Collision Detection

At first, I tried making the collision shape a cube, as this was what made the most sense to me. However, I soon realized that detecting if two cubes collide isn’t too trivial especially when considering that either cube could be rotated around any of the axes. Thus, I decided to fall back on spheres.

Calculating if two spheres are colliding is much more trivial because they aren’t affected by rotation. This simple property of spheres allowed me to detect collision easily:

Get coordinates of the center of the two spheres:

\begin{align*} p_1 &= (x_1, y_1, z_1) \\ p_2 &= (x_2, y_2, z_2) \end{align*}

Compute the distance between $p_1$ and $p_2$ :

\begin{align*} d &= \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \end{align*}

Calculate the sum of radii: $R$ .
If $d$ is less than $R$ , then the two spheres are colliding.

This is what the previous 4 steps look like in code form:

fn detect_collisions(
    mut collide_event: EventWriter<CollideEvent>,
    colliders: Query<(Entity, &GlobalTransform, &Collider)>,
) {
    let colliders: Vec<(Entity, &GlobalTransform, &Collider)> = colliders.iter().collect();
    for (i, (entity_a, transform_a, collider_a)) in colliders.iter().enumerate() {
        for (entity_b, transform_b, collider_b) in colliders.iter().skip(i + 1) {
            let distance = transform_a.translation.distance(transform_b.translation);
            if distance < collider_a.0 + collider_b.0 {
                collide_event.send(CollideEvent {
                    entity_a: *entity_a,
                    entity_b: *entity_b,
                });
            }
        }
    }
}

Rotation is not involved in any of the computations!

Rendering Collision Shapes

As mentioned earlier, the main reason why I didn’t use the heron library was due to its (temporary) incapability in rendering 3D collision shapes. So, in addition to implementing collision detection, I also added a way to render colliders in-game. I wrote the rendering functionality as a separate plugin, so colliders will still register collisions despite not being visually rendered.

I rendered the collision shapes by rendering a PBR entity with an Icosphere mesh.

In my plugin, a single PBR entity is attached to a single collider. However, I needed to attach the PBR entity as a child dynamically because the user of the plugin shouldn’t have to worry about spawning a PBR entity in their code. So, I created a system to add a PBR entity to each collider that does not already have a PBR entity. I did this by creating a component named Visible. After adding a PBR entity to a collider, I added the Visible component to the collider as a way to mark that it is already visible. Here is what the system looks like:

#[derive(Component)]
struct Visible;

fn render_colliders(
    mut commands: Commands,
    mut meshes: ResMut<Assets<Mesh>>,
    colliders: Query<(Entity, &Collider), Without<Visible>>,
) {
    for (entity, collider) in colliders.iter() {
        commands
            .entity(entity)
            .with_children(|parent| {
                parent.spawn_bundle(PbrBundle {
                    mesh: meshes.add(Mesh::from(shape::Icosphere {
                        radius: collider.0,
                        ..shape::Icosphere::default()
                    })),
                    ..PbrBundle::default()
                });
            })
            .insert(Visible);
    }
}

The key here is that the colliders query has the Without<Visible> filter.

Here is what the game looks like with the debug plugin activated:

Awesome!